Aug 25
设X是一个有限集，X的一个对自身的置换可视为一个函数，根据鸽巢原理，f ： X -> X是满的。
不经意间见到可爱的鸽巢MM。{
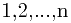}的所有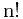
个置换构成的集合记为Sn。置换满足结合律，但不满足交换律。恒等置换就是自身不变的置换。
如果Sn中的置换的非空子集G满足如下三条性质，则定义它为X的一个置换的群，简称置换群：
i）（合成运算的封闭性）对G中所有的置换f与g，f。g也属于G。
ii）（单位元）Sn中的恒等置换属于G。
iii）（逆元的封闭性）对G中的每一个置换f，它的逆f-1也属于G。
Sn称为n阶对称群。
设Ω是一个几何图形，Ω到它自身的一个（几何）运动称为Ω的一个对称。
每个对称可看作是角点（或顶点）、边及三维情形下的面上的一个置换。
两个对称的合成仍得一个对称，一个对称的逆也是一个对称，使所有对象固定不动的运动也是一个对称即恒等对称。
Ω的对称就是它的角点上的置换群GC、边上的置换群GE以及Ω是三维情形下的面上的置换群GF。因此由图形的所有对称决定的置换集合自然是一个置换群，从而得到了角点对称群、边对称群、面对称群等等。
正n角形的（角点）对称群，除n个旋转外，还有n个反射。如果n为偶数，则有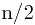
个关于对角点的反射和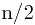个关于对边中点连线的反射。如果n为奇数，则有n个关于角点与其对边中点的连线的反射。
